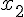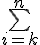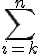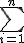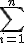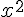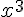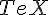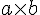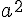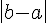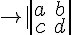Math Notation Help
Special | A | B | C | D | E | F | G | H | I | J | K | L | M | N | O | P | Q | R | S | T | U | V | W | X | Y | Z | ALL
\ |
|---|
\_ (where _ is blank)
| ||
\, | ||
\; | ||
\: | ||
\/ (backslash slash) | ||
\~ | ||
\hspace{n} | ||
\LARGE (all capital letters) | ||
\Large (L capital letter) | ||
\large (all lower case letters) | ||
\normalsize | ||
\qquad | ||
\quad | ||
\small | ||
\tiny | ||
A |
|---|
absolute font sizes (overview) | |
algebraic expressionusing @@@ x=y^2@@@ to create @@ x=y^2@@ | ||
alpha (lower case greek letter) | |
angle bracket | |
arithmetic operations | |
array | ||
B |
|---|
beta (lower case greek letter) | |
big sum | |
braces | |
C |
|---|
cdot (multiplication) | |
chi (lower case greek letter) | |
constants | |
coproduct
\symbolname_{lowerexpression}^{upperexpression}
$$\bigcoprod_{i=k}^{n}$$ gives
$$\LARGE\bigcoprod_{\small{i=k}}^{\small~n}$$ gives | ||
D |
|---|
delimiters (overview)
Note: The delimiters are automatically sizes. | ||||||||||||||||||||||||||||||||||
delta | ||
Delta (upper case greek letter) | |
delta (lower case greek letter) | ||
div (division) | |
division@@@1/2@@@ is @@1/2@@ | ||
double vertical line (norm symbol) | ||
E |
|---|
epsilon (lower case greek letter) | |
equals@@@x=2@@@ is @@x=2@@ | ||
escaping the TeX filter
| ||
eta (lower case greek letter) | |
F |
|---|
formula box | ||
fraction | ||
G |
|---|
gamma (lower case greek letter) | |
Gamma (upper case greek letter) | |
greater than@@@x>y@@@ is @@x>y@@ | ||
greater than or equal | ||
greek letters (overview)Simply write \greekletter for lower case and \Greekletter for upper case. Here's a list of all known greek letters (Note: not all upper case greek letters are known): Lower Case Greek Letters:
Upper Case Greek Letters:
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
I |
|---|
infinity | ||
integral
\symbolname_{lowerexpression}^{upperexpression}
$$\bigint_{0}^{\infty}$$ gives and $$\int_{0}^{\infty}$$ gives
$$\LARGE\bigint_{\small0}^{\small\infty}$$ gives and $$\large\int_{\small0}^{\small\infty}$$ gives | ||
iota (lower case greek letter) | |
K |
|---|
kappa | |
L |
|---|
lambda (lower case greek letter) | |
Lambda (upper case greek letter) | |
Learning Formula | ||
left only brace | |
less than | ||
less than or equal | ||
M |
|---|
Math HelpI read over the glossary. -ctd | |
math spacesList of predefined spaces:
Note: Simple blank spaces and tildes (~) are ignored by the TeX filter and don't produce any space. You must use one of the defined math spaces to get a visible (extra) space. | ||||||||||||||||||||||||||||||||||
mathematics expression | ||
matrix
Note in the example above that "lcr" has the effect that column 1 is left aligned, column 2 centered and colums 3 right aligned. | ||
minus | ||
minus plus | |
mu (lower case greek letter) | |
multiplication | ||
multiplication (with cdot) | ||
N |
|---|
not equal@@@x<>y@@@ is @@x<>y@@ | ||
nu (lower case greek letter) | |
O |
|---|
omega (lower case greek letter) | |
Omega (upper case greek letter) | |
omikron (lower case greek letter) | |
P |
|---|
parentheses | |
phi (lower case greek letter) | |
Phi (upper case greek letter) | |
pi | ||
pi (lower case greek letter) | |
Pi (upper case greek letter) | |
plus | ||
plus minus | |
product
\symbolname_{lowerexpression}^{upperexpression}
$$\bigprod_{i=k}^{n}$$ gives and $$\prod_{i=k}^{n}$$ gives
$$\LARGE\bigprod_{\tiny{i=k}}^{\tiny{n}}$$ gives and $$\large\prod_{\small{i=k}}^{\small{n}}$$ gives | |
psi (lower case greek letter) | |
Psi (upper case greek letter) | |
R |
|---|
relativity | ||
rho (lower case greek letter) | |
right only brace | |
root | ||
S |
|---|
s.u.m | ||
sigma (lower case greek letter) | |
Sigma (upper case greek letter) | |
smiley | ||
square bracket | |
square root@@@sqrt{x}@@@ is @@sqrt(x)@@ | ||
subscript | ||
sum (summation)
\symbolname_{lowerexpression}^{upperexpression}
$$\bigsum_{i=k}^{n}$$ gives and $$\sum_{i=k}^{n}$$ gives
$$\LARGE\bigsum_{\small{i=1}}^{\small{n}}$$ gives and $$\large\sum_{\small{i=1}}^{\small{n}}$$ gives | ||
superscript | ||
T |
|---|
tau (lower case greek letter) | |
TeX | ||
theta (lower case greek letter) | |
Theta (upper case greek letter) | |
times | |
triangle | ||
triggering the TeX filter | ||
U |
|---|
upsilon (lower case greek letter) | |
Upsilon (upper case greek letter) | |
V |
|---|
varepsilon (special lower case greek letter) | |
variables | |
varphi (special lower case greek letter) | |
varpi (special lower case greek letter) | |
varrho (special lower case greek letter) | |
varsigma (special lower greek letter) | |
vartheta (special lower case greek letter) | |
vertical line (absolute value, determinant, ...etc. symbol) | ||
X |
|---|
xi (lower case greek letter) | |
Xi (upper case greek letter) | |
Z |
|---|
zeta (lower case greek letter) | |
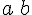
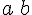
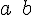
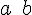
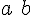
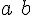
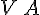
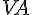
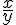
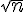
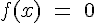

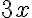
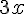
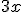
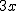
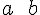
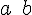
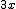
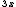
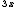
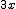
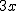
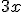
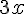
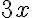
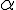

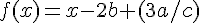
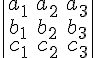
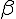
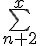
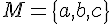
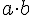
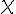
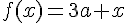
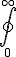
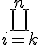
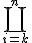
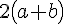
![\left[a^2+b^2~\right] \left[a^2+b^2~\right]](https://moodle.trinitydc.edu/filter/tex/pix.php/ad294afe2a577ffb993175209d64eb1d.gif)
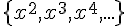
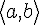
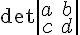
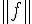
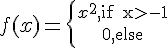
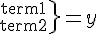
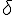
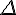
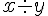
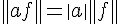
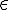
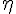
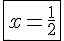
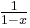
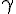
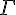
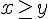
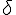
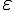
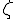
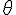
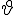
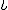
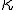
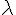
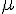
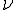
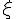
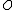
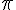
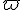
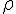
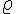
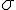
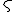
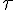
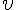
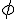
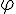
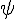
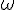
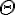
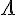
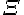
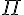
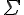
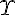
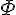
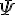
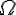
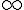
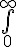
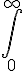
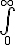
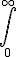
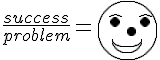

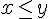
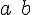


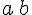
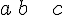
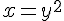
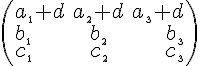

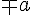
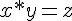

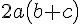
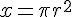

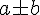
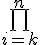
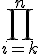
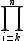
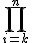
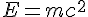
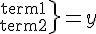
![\sqrt[3]{8} \sqrt[3]{8}](https://moodle.trinitydc.edu/filter/tex/pix.php/a075dc418402aa10b976c5619f526a8f.gif)
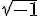
![\sqrt[n]{\frac{x^n-y^n}{1+u^{2n}}} \sqrt[n]{\frac{x^n-y^n}{1+u^{2n}}}](https://moodle.trinitydc.edu/filter/tex/pix.php/e2e1adb62f22269209aeaed8e71d40a3.gif)
![\sqrt[3]{-q+\sqrt{q^2+p^3}} \sqrt[3]{-q+\sqrt{q^2+p^3}}](https://moodle.trinitydc.edu/filter/tex/pix.php/d33ba3b5acab8d2b62117e83ed9f7956.gif)
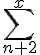

![\left[a,b\right] \left[a,b\right]](https://moodle.trinitydc.edu/filter/tex/pix.php/22be842f9527b4b0ef3b7085b5486b7b.gif)